Math | Digital Wealth

Benford’s law – how to detect fraud through numbers

How to detect problems pertaining to randomness of numbers using Benford’s law. The theory can be used to detect fraud, evasion of rules etc.

Suppose you have some financial data – let us say all the vouchers paid by the company in a given month, and you want to run some tests to determine if there are any anomalies. For example, are the employees beating the approval process by entering say $24.99 vouchers if the limit is $25, or if any fraud is being committed. One way to do this is to use Benford’s law.

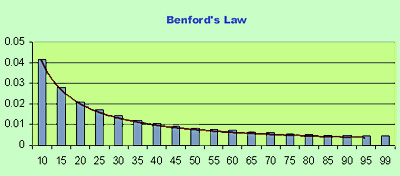
Benford’s law states that in a given list of numbers generated naturally (for example stock prices or census figures), the probability of a number starting with 1 is 30.1%. The probability of a number starting with 2 is 17.6% and so on – it keeps decreasing as the numbers increase. The rationale behind it is explained as: it takes a 100% increase to take a number from 100 to 200. However, it takes only a 50% change to go from 200 to 300. 100% increase is more difficult to do (and thus has less probability of happening) than a 50% increase.

In this way, the probability of having a number starting with digit d is given by log(1+1/d), log to base 10. More information is available here. Its usually extended to the first two digits for analysis in the real world.

Download from here a spreadsheet (called Numeric Truth) to carry out this analysis for you. All you have to do is to paste your data into the green cells. After that, on the first sheet it will show the results of first digit analysis, and on the second sheet, two digit analysis. Have a look at the graph, the variances for the individual digits, and the total variance. That should give you a starting point for your analysis/audit.

Testing for primality

How to test a huge number for primality? Provides an implementation of the famous Miller-Rabin algorithm using the widely available ‘bc’ (basic calculator) tool. Suitable both for Linux and Windows.

Testing if a number is prime is an interesting problem. Prime numbers have uses in many fields especially Cryptography. Here we show a technique through which we can verify if a number is prime or composite (not with 100% guarantee though). The algorithm we use is called Miller-Rabin.

I have, in another blogpost, talked about a tool available on Unix called bc which stands for basic calculator. In truth, its not ‘basic’ by any stretch of imagination. For my Windows brethren, a version is part of UnxUtils. This tool allows you to do large number, arbitrary precision calculations. It also allows you to write scripts. The script to implement this test is called pcheck.bc.

On Unix, it can be run using ./pcheck.bc while on windows it needs to be run like this:

bc pcheck.bc -ql.

The '-l' option is for bc to load math. library, and the '-q' option is to stop bc from boasting when it runs.

First, it will ask you for an option. The algorithm runs in iterations, each iteration requiring the given number (called p) to be tested against another number from a set (called s). If p is composite against s, then p is composite else p is probably prime. In order to increase this probability, this implementation tests against 30 given numbers. If option is entered as ‘0’, the program will read the numbers in set from the input and you can enter the numbers suitably. If its entered as ‘1’, the program will automatically select the set. If you are able to enter random numbers then select option ‘0’ else select ‘1’. I may talk about generating arbitrary long random numbers in a future blogpost.

Second, it will ask you for the number to test. Enter any large odd number (even numbers are composite). Sample:

900900900900990990990991 (prime)
900900900900990990990993 (composite)
359334085968622831041960188598043661065388726959079839 (prime)

Third, if you selected option ‘0’, it will prompt you for the 30 random numbers.

Read the code to understand further – its not very difficult to understand. Have questions, post comments.

This can be further extended to search for primes: start at any big odd number, test it – it its prime report and stop, if not add 2 to the number and test again. I used this code to search for very large primes. In fact, I used it to prove 2^600-95 is a 181 digit prime.

Value of Pi

Wikipedia defines Pi or p as “a mathematical constant which represents the ratio of any circle’s circumference to its diameter in Euclidean geometry”. As a kid I used to be interested in the calculation of Pi. The value of Pi, to 100 places of decimal is:

3.1415 9265 3589 7932 3846 2643 3832 7950 2884 1971 6939 9375 1058 2097 4944 5923 0781 6406 2862 0899 8628 0348 2534 2117 0664

I have calculated this using the Unix command bc. The command for this is based on an identity (that I think is credited to Ramanujan) and is:
24*a(1/8)+8*a(1/57)+4*a(1/239)
where a stands for the arctangent function.

The formula is:
pi = 24*arctan(1/8)+8*arctan(1/57)+4*arctan(1/239)

First, load the bc language with associated library using “bc -l”. Then, set the scale to the number of digits using “scale=100”. Afterwards run the identity I gave above.

To experimentally calculate Pi experimentally, there are two ways: One using a random number generator and the other by physically measuring the circumference of a given circle.

Consider a square of length unity. Within that, a circle is drawn, having unity diameter. If a point is taking within the square at random, the probability of that point also lying within the circle is Pi*(1/2)*(1/2) which is Pi/4. Now, start taking points at random (x,y) and see if x*x+y*y<=1/4 or not (if it is, then that means the point lies within the circle). Maintain the count of total number of points taken (t), and the number that fell within the circle(c). Now Pi can be calculated as:

Pi=4*c/t

The other method is to take a circular bottle (measure the radius r) or tin and tie a thread around its circumference. Measure the circumference(c). Now Pi is c/2r.

The following two sentences contain the value of Pi: the number of letters in each word indicates the corresponding number in the value of Pi.

1. “May I have a large cup of coffee.”

2. “How I want a drink, alcoholic of course, after the heavy chapters involving quantum mechanics.”

This makes the value of Pi easy to remember.

Lastly, how useful are the digits of Pi as a source of random numbers? Not bad, according to a study: “while sequences of digits from pi are indeed an acceptable source of randomness – often an important factor in data encryption and in solving certain physics problems – pi’s digit string does not always produce randomness as effectively as manufactured generators do”.

Always wanting to do my own thing, I downloaded the value of Pi to one million places from a website, split it into (x,y,z) coordinates, each having 5 digit precision. Here is the graph that got generated:

A bell curve, but could have been better – seems to mimic the results from the study.

Continuous Compounding

I feel there is something mathematically wrong with the way compound interest is defined today. We say “5% per annum, semi-annually compounded”. If I have money invested, mathematically speaking, it should get compounded all the time, not just in fixed intervals.

I would like to define the term “absolute percentage” – the annual interest rate at which the money must grow all the time in order to reach the same amount as it does using normal interest rate calculation. Let me explain what that means.

If I invest amount ‘p’ for period ‘t’ years, at an ‘absolute’ interest rate of ‘rdash’, then,

a=p*e^(rdash*t/100)

where ‘e’ is a mathematical constant having value approximately 2.71828182845904.

This means, that amount ‘p’ will grow to amount ‘a’ in ‘t’ years if it compounds continuously.

Here, rdash is the absolute equivalent of rate r if
a=p*(1+r/100)^t

Here is a table that explains it. Try and understand, ok?